Introducción
En esta unidad didáctica, vamos a explorar el concepto de diagrama de árbol. Los diagramas de árbol son una herramienta útil en muchos campos, desde la matemática hasta la biología y la ingeniería. A lo largo de esta unidad, vamos a examinar en detalle lo que es un diagrama de árbol, cómo se construye y cómo se utiliza. Al final de esta unidad, los estudiantes deberían tener una comprensión sólida del concepto y estar preparados para utilizar los diagramas de árbol en una variedad de contextos.
Objetivos de aprendizaje
- Comprender el concepto de diagrama de árbol.
- Aprender a construir un diagrama de árbol.
- Aprender a utilizar un diagrama de árbol para resolver problemas.
Contenido
Parte 1: ¿Qué es un diagrama de árbol?
Un diagrama de árbol es una herramienta gráfica que se utiliza para representar las posibles ramificaciones de una situación. Se parece a un árbol invertido, con una línea central que representa el evento principal y ramas que se extienden desde la línea central para representar las diferentes opciones que pueden surgir a partir del evento principal. Los diagramas de árbol se utilizan comúnmente en la teoría de la probabilidad y en la toma de decisiones.
Parte 2: Cómo construir un diagrama de árbol.
Para construir un diagrama de árbol, se debe seguir los siguientes pasos:
- Paso 1: Identificar el evento principal. Este es el evento que se está investigando. Por ejemplo, si estamos investigando la probabilidad de que una moneda caiga cara o cruz, el evento principal es «lanzar la moneda».
- Paso 2: Identificar las opciones que pueden surgir a partir del evento principal. En el ejemplo de la moneda, las opciones son «cara» o «cruz».
- Paso 3: Para cada opción identificada en el paso 2, identificar las opciones adicionales que pueden surgir. Por ejemplo, si la moneda cae cara, la opción adicional es «lanzar la moneda de nuevo».
- Paso 4: Continuar el proceso hasta que todas las opciones hayan sido exploradas.
Parte 3: Cómo utilizar un diagrama de árbol para resolver problemas.
Los diagramas de árbol se pueden utilizar para resolver una variedad de problemas. Para resolver problemas utilizando un diagrama de árbol, se debe seguir los siguientes pasos:
- Paso 1: Identificar el evento principal. Por ejemplo, si estamos investigando la probabilidad de que un estudiante apruebe un examen, el evento principal es «el estudiante toma el examen».
- Paso 2: Construir un diagrama de árbol. Utilizando el proceso descrito en la Parte 2, construir un diagrama de árbol que muestre todas las posibles ramificaciones que pueden surgir a partir del evento principal.
- Paso 3: Asignar probabilidades. Asignar probabilidades a cada opción en el diagrama de árbol. Por ejemplo, si la probabilidad de que un estudiante apruebe un examen es del 70%, se asigna un 70% a la rama correspondiente.
- Paso 4: Calcular la probabilidad de los resultados
Una vez que se ha construido el diagrama de árbol y se han asignado las probabilidades, se pueden calcular las probabilidades de los resultados que se desean analizar. Por ejemplo, si se desea calcular la probabilidad de que un estudiante apruebe el examen, se deben sumar las probabilidades de todas las ramas que llevan a un resultado de aprobación. Si se desea calcular la probabilidad de que un estudiante repruebe el examen, se deben sumar las probabilidades de todas las ramas que llevan a un resultado de reprobación.
Parte 4: Ejemplo de aplicación de un diagrama de árbol
Supongamos que se desea analizar la probabilidad de que una familia tenga dos hijos y al menos uno de ellos sea niña. Para resolver este problema, se puede construir un diagrama de árbol como se muestra a continuación:
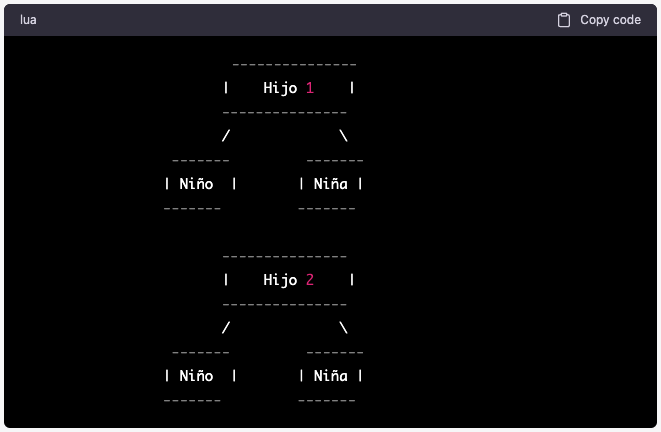
En este diagrama de árbol, el evento principal es «tener dos hijos». Las opciones son «niño» o «niña». Para cada opción, se considera la probabilidad de tener otro niño o niña. La probabilidad de tener un niño o una niña es del 50%.
Para calcular la probabilidad de que al menos uno de los hijos sea niña, se deben sumar las probabilidades de las ramas que llevan a este resultado. Estas son las ramas que representan tener una niña y cualquier combinación de niños y niñas. En este caso, hay tres ramas que cumplen este criterio: la rama que representa tener dos niñas, la rama que representa tener una niña y un niño, y la rama que representa tener un niño y una niña. Cada una de estas ramas tiene una probabilidad de 0.25. Por lo tanto, la probabilidad de que al menos uno de los hijos sea niña es del 0.75 o del 75%.
Actividades
Actividad 1. Construyendo un Diagrama de Árbol
Objetivo. Que los estudiantes aprendan a construir un diagrama de árbol.
Materiales. Papel, lápiz.
Instrucciones:
- Proporciona a los estudiantes un problema que pueda ser resuelto mediante un diagrama de árbol, como por ejemplo, la probabilidad de que una moneda caiga cara o cruz en dos lanzamientos.
- Pide a los estudiantes que construyan un diagrama de árbol para resolver el problema.
- Una vez que los estudiantes hayan terminado sus diagramas, discute el proceso de construcción del diagrama de árbol en grupo, revisando cada paso y aclarando cualquier duda que pueda surgir.
- Haz que los estudiantes compartan sus diagramas de árbol con la clase para que puedan comparar y contrastar las diferentes soluciones.
Actividad 2. Resolviendo Problemas con Diagramas de Árbol
Objetivo. Que los estudiantes aprendan a utilizar los diagramas de árbol para resolver problemas.
Materiales. Papel, lápiz.
Instrucciones:
- Proporciona a los estudiantes un problema que pueda ser resuelto mediante un diagrama de árbol, como por ejemplo, la probabilidad de que una familia tenga dos hijos y al menos uno de ellos sea niña.
- Pide a los estudiantes que construyan un diagrama de árbol y que calculen la probabilidad de los resultados deseados.
- Una vez que los estudiantes hayan terminado sus cálculos, discute el proceso de cálculo de probabilidades en grupo, revisando cada paso y aclarando cualquier duda que pueda surgir.
- Haz que los estudiantes compartan sus resultados con la clase para que puedan comparar y contrastar las diferentes soluciones.
Actividad 3. Tomando Decisiones con Diagramas de Árbol.
Objetivo. Que los estudiantes aprendan a utilizar los diagramas de árbol para tomar decisiones informadas.
Materiales. Papel, lápiz.
Instrucciones:
- Proporciona a los estudiantes un escenario en el que se deba tomar una decisión, como por ejemplo, decidir si deben comprar un seguro para un viaje en avión.
- Pide a los estudiantes que construyan un diagrama de árbol que muestre las posibles ramificaciones de la decisión, como por ejemplo, las posibles situaciones que podrían ocurrir en el viaje en avión.
- Pide a los estudiantes que asignen probabilidades a cada opción y que calculen la probabilidad de los resultados deseados, como por ejemplo, la probabilidad de tener un accidente aéreo si no se compra un seguro.
- Una vez que los estudiantes hayan terminado sus cálculos, discute en grupo las diferentes opciones y los resultados de las probabilidades calculadas, para que puedan tomar una decisión informada.
Conclusión
Los diagramas de árbol son una herramienta valiosa para analizar problemas y tomar decisiones en muchos campos, desde la matemática hasta la biología y la ingeniería. Construir un diagrama de árbol es un proceso sistemático que ayuda a visualizar las posibles ramificaciones de una situación. Para utilizar un diagrama de árbol, se deben asignar probabilidades a cada opción y luego calcular la probabilidad de los resultados deseados. Los diagramas de árbol son una herramienta poderosa para analizar problemas de manera sistemática y tomar decisiones informadas.